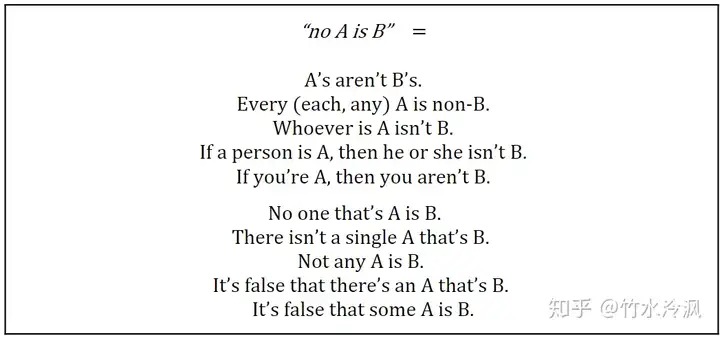逻辑学：从入门到入土（二）——三段论


作者：竹水泠沨
仍然先举一个例子：

所有金属都可以导电。铜是金属。
∴铜可以导电。

上面这个论证过程，就是非常经典的三段论的一个例子。三段论的特征是用“all”，“some”和“no”进行论证，由亚里士多德首先提出。在传统逻辑中，它指的是一个命题（结论）必然地从另外两个命题（前提）中得出。

传统逻辑，也叫做词项逻辑，是关于亚里士多德（公元前384年—前322年）所开创的传统逻辑学的宽松的术语，并有幸的没有经历广泛的改变，直到十九世纪末出现了谓词逻辑，也就是符号形式系统的通用术语。——来源喂鸡百科
现在创造一个“三段论语言”，来对上面的例子进行改写：

all 金属 is 导电铜 is 金属
∴铜 is 导电

再进行进一步的简化：

all J is Dt is J
∴t is D

在三段论语言里，一般用大写字母来表示一般类别（金属、导电），用小写字母表示特殊个体（铜）。在三段论的公式里，除了将特殊个体一般化的字母以外，还会使用五个词：all，no，some，is，not。用这些词和字母组成的语法句子被称为wffs，即well-formed formulas。wffs有以下八种形式（注意大小写）：

除了上图出现的语句以外任何语句都不是wffs，同样，如果字母的大小写与上图不符，则也不属于wffs。

当wffs以小写字母开头时，后面的字母既可以是大写也可以是小写。而当wwfs以大写字母开头时，后面只能跟大写字母。

举个例子：

小明是数学很好的人。 ⇒ x is H

小明是学校里数学最好的人。 ⇒ x is h

有些猫很高冷。 ⇒ some M is G



思考题：

请将下列一般语句转换为wffs：

这本书是绿色的。所有人都不开心。澳洲是大陆。澳洲是最小的大陆。善的概念本身就是善的。
知道了三段论的基本规则之后，就可以对三段论的有效性进行检验了。在此之前要先了解一个概念：周延。周延的项只跟在“all”或“no/not”后面。

如果一个范畴项被称为是周延（distribute）的，那么表明这个范畴的所有个体都被涉及到。在陈述如“所有 A 不是 B 就是 C”中，项 A 是周延的，因为集合 A 的所有元素都被指出了。而项 B 和 C 不是周延的，有的 B 和 C 不是 A。
在陈述如“某些 D 是 E”中，D 和 E 都是不周延的，因为没有提及余下的（不是 E 的 D 和不是 D 的 E）。——来源喂鸡百科

有下划线的字母即为周延的项
检验三段论有效性的方法叫star test，其具体过程如下：

将周延的项画上下划线；将前提里有下划线的项标星号，结论里没有下划线的项标星号；当每项刚好被标星了一次，且（be的）右边刚好只有一个星号时，推理是有效的。

那假如说，我们要对以下论证进行检验：

每个人（R）都有一死（Y）只有人（R）才能被称之为哲学家（Z）
∴每个哲学家（Z）都有一死（Y）

将其转换成三段论语言：

all R is Yall Z is R
∴all Z is Y

在这里我们需要将“每个”和“只有”转换成三段论语言“all”“no”和“some”。很明显“每个”的意思就是“all”，但“只有”就有点微妙了。从整个句子上来看，“只有人才能被称之为哲学家。”真正的含义是“所有（all）哲学家都是人。”所以将其转换为三段论语言就是“all Z is R”。

下面是一些常见的表示“all”的句式：

然后是“no A is B”和“some”的常见表达方法：

这里注意不能写成“all A is not B”，因为它不符合wffs的任何一种形式。

在逻辑学中有三条基本规律，即同一律，矛盾律和排中律。简单地来说，同一律要求在同一思维过程中，一个思想必须保持其确定和同一，矛盾律要求一个思想及其否定不能同时是真的，排中率要求在同一思维过程中，两个互相矛盾的思想不能同时是假的。

套用到wffs里可得出：“all A is B”和“some A is not B”两者不能同时为真。同理“some A is not B”和“no A is B”两者也不能同时为真。

到目前为止，我们的论点都是用一种明确的前提&结论格式表述的。实际上，现实生活中的争论很少如此干净利落。相反，我们可能会发现令人费解的措辞或无关的材料，而关键的前提可能被省略或只是暗示，因此我们很难找出前提和结论。这时候就需要对文章的句子进行简化，对句子结构进行分析，这样才能更好地进行有效性的验证。举例：

“你（Y）不能（N）进，只有会员（H）才能进来。”

如果直接简化的话就会变成：

all N is H

∴Y is not N

这显然是不对的。

在这句话里，蕴含了一个隐藏前提，即“你不是会员。”如果加上这个隐藏前提的话就会变成：

all N is HY is not H
∴Y is not N

star test证明有效。

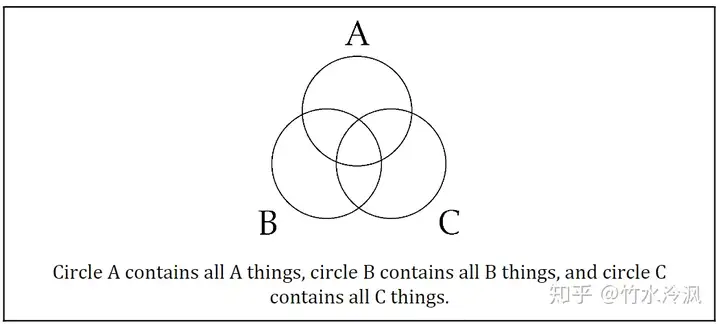
除了star test之外，书中还介绍了另一种检验有效性的办法，即维恩图。

这个东西就是维恩图
方法很简单，根据前提，用不同的符号把重叠的部分和被排除的部分标起来，然后将其与结论对照即可验证有效性。
《INTRODUCTION TO LOGIC》中检验三段论的 the star test是什么意思？
这个回答举出了一些star test检验无效但维恩图检验有效的例子。只要留意这些形式，star test就会是一个很好用的检验方法。

此外，以亚里士多德为代表的传统的逻辑学派和现代逻辑学派在某些三段论的有效性上有一些争议，其主要体现在对empty term（不涉及任何存在的一般术语）的观点不同。举例：

比较以下两个论证：

所有猫是动物。
∴有些动物是猫

2. 所有独角兽是动物。

∴有些动物是独角兽。

从直觉上看，第一个好像是有效的，而第二个不是，因为一般认为独角兽并不真正存在。但它们的形式是一样的，用star test检验后可以发现两个论证都是无效的。

当我们读到第一个论点时，我们倾向于假设世界上至少有一只猫。假定这是一个附加的前提，就可以得出一些动物是猫的有效结论。而当我们读第二个论点时，我们并没有假设世界上至少有一只独角兽。如果没有这个额外的假设，就不能推断出有些动物是独角兽这个结论。

所以，如果我们假设C存在，那么"all C is A ∴ some A is C”则是有效的，反之则无效。亚里士多德认为，三段论中的每一个一般术语都涉及到至少一个存在的生物，因此这个论证是有效的。而现代观点允许像“独角兽”这样的empty term的存在，所以认为"all C is A ∴ some A is C”的论证过程是无效的。