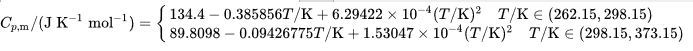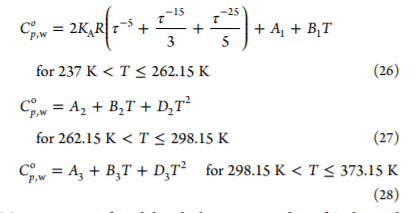一升100度的水倒入一升0度的水，是不是就是两升50度的水？


嗯，两杯水都是一升，所以一样重。热量从开水到凉水，吸收的热量等于放出的热量。

所以最后的温度就是两杯水平均。（100+0）/2=50℃，完美！


看看这「1+1=2」的问题，怎么会为难我这个小天才？结果一旁的温度计提醒我：

好像有什么东西不太对？

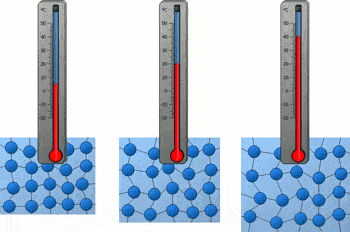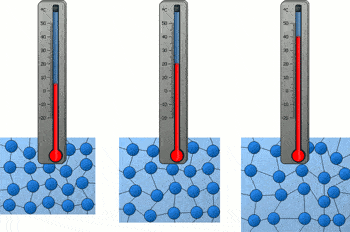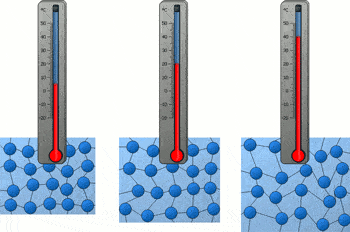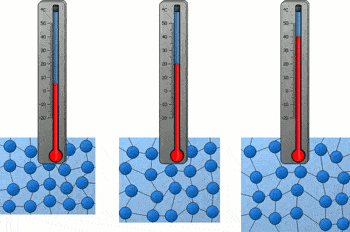
温度计的原理很简单，「热胀冷缩」：温度高了里面的水银跑的老高，温度低了老老实实的缩回去。


如果这两杯水也像水银一样热胀冷缩的话，开水的体积是不是比冰水大啊？

「热胀冷缩」这个概念可能不那么黑科技，我们放大放大再放大，把水分成水滴，再把水滴里面的一个个小分子拿出来看。


（一个标准的水分子）

一杯水具有的能量，与这杯水拥有的分子数量有关。温度越高，分子拥有的能量越多。这些分子又在不停的运动，这些能量就表现为动能，温度高了，移动速度就快了。

温度低的时候，天气冷，这些小分子只能在小房间里抱团取暖。温度高了，热量增加，这些小分子暖和了。之前抱团的小分子，就会像疫情「解封」一样，带着热量到处撒欢。


既然要到处撒欢，活动的地方就不是小房间了。最不济，得找个地方跳跳广场舞吧？


由于小分子要活动的地方变大了，所以温度高的水里面，是更少分子数的水，占了更多的地方。

我们用红墨水标记热水，接着用蓝墨水标记冷水。

热水和冷水混合后，是热水先飘在上面。这也表明了相同体积下，热水的密度相对冷水更小。

如果用物理名词来说，就是「质量不变的前提下，水的温度越高，体积越大，密度越小。」


如果是一样体积的开水和冰水混合，那么开水就少了一点份量。

既然质量不同，混合之后水的分子数就不是单独一杯水的两倍，传递的能量也不是对半分。

所以，最后这杯水的温度，肯定不是50度。

既然答案不是「50度」那么简单，我们应该怎么继续确定混合后水的温度呢？

这个时候就要介绍一下「比热容」这个概念了。

这个概念是「没有相变化和化学变化时，1kg均相物质温度升高1度所需的热量」。


听起来太复杂了，我们再把这个概念简化一下。

每个人都要吃一日三餐，但是胃口好不好，是一门玄学：

心情好了，之前运动过，胃口就会好，吃的也很多；吃饭前吃了零食，或者生了病，胃口就不好，吃的也就少。


如果我们把吃的食物看成「热量」，把影响胃口的因素看成「影响吸收热量的条件」。

那么「比热容」就是吸收热量的「胃口」。


考虑到装水的杯子和水周围的空气都有可能影响热量，我们假设「热水放出的热量=冷水吸收的热量」，由于「热胀冷缩」，所以要重新确定密度。

100kPa下0度水密度为0.99986g/cm³，100度水密度为0.95840 g/cm³。

代入计算之后，得出来的结果是48.9414℃。

这杯水虽然比较烫，但是稍微晾晾喝起来还不错。

一升100度的开水，加上一升0度的冰水，最后温度果然不是50度。


但是「比热容」这个新概念又开始让人头大：

之前我们比热容当作可能变化的「胃口」，但是刚才的计算是在比热容不变的前提下得出的。

那么比热容在「冷热交加」的情况下，真的会「不动如山」吗？


没错，比热容的确会随着温度的变化而变化！而且比热容也可以根据温度进行推算！


这个式子太费劲了，宝宝算不出来啊！


简单来说，计算过程就是继续沿着「热水放热=冷水吸热」的思路，把容易受到温度干扰的质量和密度，换成了不会因为温度变化的「物质的分子量」。

最后算出来的混合温度是48.98℃，比一开始算的稍微高一点点。

当然由于水的热胀冷缩，混合之后的水肯定不是两升温水。

最后混合的水，体积要比两升小一点，大概是1.98升。


实际上，对于这个看似简单的「开水兑凉水」的提问，有许多正儿八经的论文进行过论述，针对水的「密度」还有「比热容」的变化函数进行了详细的计算。


虽然我们得到了精确的结果，但是看到这里，肯定会人觉得这样的「刨根问底」有点太复杂。

当然了，生活当中，这个问题不用过于较真。但是对于科学而言，这就不仅仅是「不较真」那么简单了。

简单的热水和冰水里面，就已经蕴含了密度，温度，热量等一系列概念。这些概念之间的相互交叉，让一个本来简单的问题，变得趣味横生。


科学探索的过程，就是搞懂这些关系，让这些概念不再虚无缥渺的探索之旅。

复杂的计算和推理终于结束了，但是这只是探索之旅的一小步。

热水和冷水之间的混合，没准也能给你的生活，带来一份探索的快乐。

最后提醒一句：天气要转凉了，多喝热水。


（文中图片素材来源自网络，仅供学习交流使用）