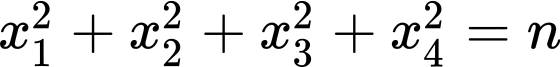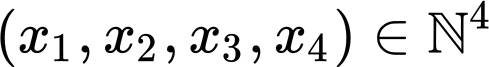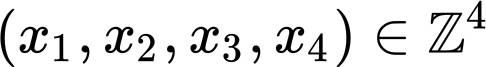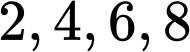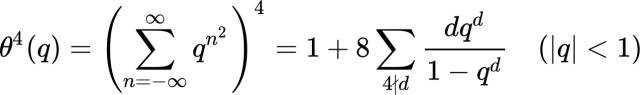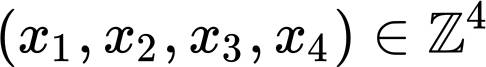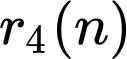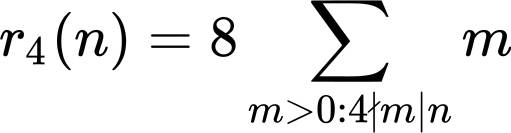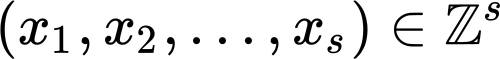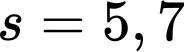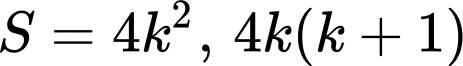“这里太小，我写不下。”费马这句话犹如塞壬之歌一般，三百多年来，蛊惑了无数数学天才，他们义无反顾地向这个定理发起挑战，但最终都无功而返。 跨越几个世纪的追寻，从欧拉到高斯，从热尔曼到狄利克雷，从拉梅到柯西，从库默尔到里贝特，甚至运用超级计算机日夜不停地运算……
直到1995年，怀尔斯站在百叶窗下，翻动《数学年刊》第141卷上最新的两篇文章——《模形椭圆曲线和费马大定理》与《某些赫克代数的环理论性质》，冷静地回味着他对全世界说的话：“让我们就在这里结束吧。”
358年的智者接力，到达终点。
——《公式之美》

1636年 法国数学家费尔马 提出四平方和定理但无力证明
1748年  (112年后）  欧拉  完成部分证明
1770年  (134年后）拉格朗日证明了费尔马所猜测的四平方和定理
。。。
。。。
站在前人的肩膀上，怀尔斯在1991年的夏天公布了自己对费马猜想的证明。可是数学家凯兹指出了怀尔斯证明中关于欧拉系的构造的严重漏洞，怀尔斯不得不思考用其他方法来填补漏洞。他想起自己先前用岩泽理论解决失败，后来又用克列瓦金-弗莱切方法试图解决该问题。于是怀尔斯将这两者结合在一起，完美地填补上了这个漏洞。终于在1995年，怀尔斯完美地证明了费马猜想，跑完了这场接力赛的最后一帮。自此，费马猜想荣升为定理，它终于可以被名正言顺地称作费马大定理了。

费马大定理这只下金蛋的母鸡为人类数学的发展立下了汗马功劳。回望这三百多年，人类每一次都用尽全力地追寻，虽然未能抵达终点，却扩充了“整数”的概念，扩展了“无穷递降法”、虚数和群论的应用，催生出库默尔的“理想数论”，促成了莫德尔猜想，证明了谷山-志村猜想，加深了对椭圆方程的研究，找到了微分几何在数论上的生长点，发现了伊利瓦金-弗莱切方法与伊娃沙娃理论的结合点，推动了数学的整体发展……

一部波澜壮阔的数学史由此徐徐展开，这是一场智者征服世间奥秘的接力赛，而信仰和追寻就是这场接力赛的最大意义。毕竟，正是因为有了这一群仰望星空的人，人类才有了希望。
我所感叹的是西方社会历史，在300多年的战乱不断的情况下，依然能给数学家一个安静的书桌，起码的体面。
而我们东方社会历史空有数千年稳定王朝，却无一人对数学进行研究。真是可惜啊。
这显然不是种族的问题，新中国成立后，中国人在数学研究搞出了巨大的成绩，有目共睹。
平方和问题简史 2019-03-05 16:55 作者 | 林开亮 陈见柯
(提示: 如果文中数字/公式显示较大, 请点击右上角中"刷新"即可恢复正常. )
数论中一个重要的课题是平方和问题，它有很长的历史。这里做一简要介绍。
韦伊（A. Weil）在其数论史著作[8]中提出，法国数学家费尔马（Fermat）为现代数论之父。关于平方和，费尔马有两项杰出工作。
第一，他在1640年指出：形如的素数 都可以写成2个整数的平方和，并进一步给出了任意一个自然数 表示为整数平方和的方法数目；
第二，他在1636年断言：每个正整数都可以写成4个平方数的和。
1
费尔马的工作吸引了欧拉（Euler），对于费尔马关于2个整数的平方和的命题，欧拉用了七年时间才给出证明。
对于与二平方和命题几乎平行的四平方和的断言，欧拉也投入了大量精力，一个关键性的突破，是他在1748年发现了著名的四平方和的乘积公式（一个特例是归功于丢番图的平方和的乘积公式）：
其中 为2
遗憾的是，欧拉没有完成证明，而把临门一脚——证明每一个素数都可以写成四个整数的平方和——留给了后起之秀拉格朗日（Lagrange）。
1770年，在欧拉工作的基础上，拉格朗日证明了费尔马所猜测的四平方和定理：对任意的正整数 ，丢番图方程

有整数解。仿照费尔马，欧拉提出了这样的问题：对任意给定的 ，求出该方程的非负整解

的个数关于 的一个公式。欧拉尝试用母函数的办法，但由于他限制于考虑正整数解，所得的母函数

丧失了对称性，最终徒劳无功。欧拉也曾建议，用母函数的方法考察费尔马关于多边形数断言的证明，他认为这是“最自然的证明方式”。然而，他也没有成功。
可喜的是，安德鲁斯（Andrews[1])后来复活了欧拉的想法，用母函数的方法重新证明了高斯的三角形数定理。
1829 年，另一位在计算方面可与欧拉相媲美的数学家雅可比（Jacobi）通过考虑上述丢番图方程的整数解

而修正了欧拉的思路，得到了满意的解答。雅可比将欧拉的母函数 对称化从而得到了著名的 函数：
利用 函数，雅可比求得了将任意给定的正整数 分别表示为

个平方数的表达数目的公式。例如，雅可比算出

由此立即可以读出不定方程

的整数解

的个数

的通式

这就引出了一个一般问题（平方和问题）：设

表示丢番图方程
的整数解

的个数，求

的显式表达式。
在雅可比之前，勒让德（Legendre，1798 年）与高斯（1801 年）分别求得了

的公式（此处从略）。雅可比的贡献在于，将椭圆函数引入到这个数论问题中，这后来成为了求解这类问题的标准方法。对于 的求解，历史上许多大数学家都有贡献，继勒让德、高斯和雅可比之后，很多大数学家作出了重要贡献，列表说明如下（见[4]）：

其中特别传奇的两个人物是闵可夫斯基（Minkowski）与拉马努金（Ramanujan）。
年仅 18 岁的闵可夫斯基比他的前辈艾森斯坦因（Eisenstein）和史密斯（H. J. Smith）更深入地解决了

的情况，可见[7]。而自学成才的拉马努金则独立发现了雅可比的 函数，他的故事可见其传记《知无涯者》[5]。
继他们之后，对更一般的二次型的算术理论作出了巨大贡献的，还有西格尔（Siegel）与志村（Shimura）。但对平方和问题，即 的求解，直到2000年左右，才取得重大进展。
首先是在 1996 年，米尔恩（Stephen Milne）迈出了突破性的进展，他对

给出了 的公式。Milne 的工作受到了卡茨（V. G. Kac）和胁本实（Minoru Wakimoto） 1994 年在研究李代数时提出的猜想的启发。
继此重要突破之后，察吉尔（D. Zagier）、刘治国、曾衡发及其合作者蔡国成、C. Krattenthaler、小野（K. Ono）等做了相关的工作。 特别值得一提的有两笔。
2003 年，曾衡发（Heng Huat Chan）与蔡国成（Kok Seng Chua）对一切偶数 成功猜测出 的公式。 之后，杨一帆（Yifan Yang）与福原真二（Shinji Fukuhara）、田坂浩二（Koji Tasaka）、德国数学家克里格（K. Kilger）等给出了三个独立的证明。
2013 年，刘治国首先给出了一个一般方法对任意的正整数 计算 ，其中 是任意的正整数。这个方法原则上将 的计算，归结为计算某些基本的超几何级数的特殊值，不过后一个问题目前还是很难。
平方和问题一度在历史上占有重要地位，例如它占据着迪克森（Dickson）的第2卷《数论史》[3] 的四章篇幅。完全可以理解，当米尔恩在1997年取得如此大的成就时，美国的《科学新闻》[6]对此作了激动人心的报道。对平方和问题更详细的介绍，见曾衡发与Krattenthaler合写的精彩综述[2]。
注释：
致谢：作者在论文准备过程中，曾与下述数学家与学者通讯并获得帮助，特表感谢：新加坡国立大学数学系曾衡发教授，台湾国立交通大学应用数学系杨一帆教授，以及华东师范大学数学系刘治国教授。
参考文献：
[1] G. E. Andrews, EREKA! num=, J. Number Theory 23 (1986) ,285–293.
[2] H.H. Chan and C. Krattenthaler, Recent progress in the study of representations of integers as sums of squares, Bull. London Math. Soc. 37(2005), 818–826.
[3] L. E. Dickson, History of the Theory of Numbers,Vol. 2: Diophantine Analysis. New York: Dover, 2005.
[4] 华罗庚，《数论导引》，科学出版社，1957年。
[5] R. Kanigel, The Man Who Knew Infinity: a Life of the Genius Ramanujan. New York: Charles Scribner’s Sons, 1991. 中译本《知无涯者》，胡乐士、齐民友译，上海科技教育出版社，2008年。
[6] Ivars Peterson, Surprisingly Square:Mathematicians take a fresh look at expressing numbers as the sums of squares, Science News, June 16, 2001; Vol. 159, No. 24, p. 382—383.
[7] C. Reid, Hilbert, Copernicus, New York, 1996. 中译本《希尔伯特》，李文林、袁向东译，上海科技出版社，2006年。
[8] A. Weil, Number Theory: An Approach through History from Hammurahi to Legendre, Birkhäuser, Boston, Mass., 1983. 中译本《数论：从汉穆拉比到勒让德的历史导引》，胥鸣伟译，高等教育出版社，2010 年。
中国的拉马努金：不为人知的传奇数学家刘治国返回搜狐，查看更多